[新しいコレクション] 扇形 弧の長さ 公式 290141-扇形 ���の長さ 公式
円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2 扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π をなぜわざわざ弧度法を使うのか、 弧度法のメリットを紹介します。 ・弧度法のメリット1つ目は、 弧の長さ,面積が簡単に求められます。 次の章「扇形の弧の長さと面積の公式」で解説するから分かるように、弧度法も用いると簡単に扇形の弧の長さと面積が求められるようになります。つまり、 扇の弧の長さは扇の中心角αの大きさに比例する ことがわかります。 扇の面積 扇の面積を「S」としたとき、Sは次の公式で求めることができます。 これも同じように、円の面積を求める公式を思い出してください。 円の面積=r² π で求めることができましたね。 すなわち、 扇の面積も弧の長さと同様、扇の中心角に比例する ことがわかります。 ・ 中学数学の図形で使う公式・定理の一覧
中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋
扇形 弧の長さ 公式
扇形 弧の長さ 公式- 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。 式を変形 小文字になってしまっていますが気にしないでください。 理由はありあません。 私のミスです。 ここで、2 r πそして、この弧度法を使った有名な公式が 扇形の弧の長さ公式と面積公式 面積公式は2つありますが、弧の長さ公式を使うことで下を導き出すことは可能。 でも、毎回導き出すのは面倒なので、2つとも覚えておくと計算がスムーズになります。




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
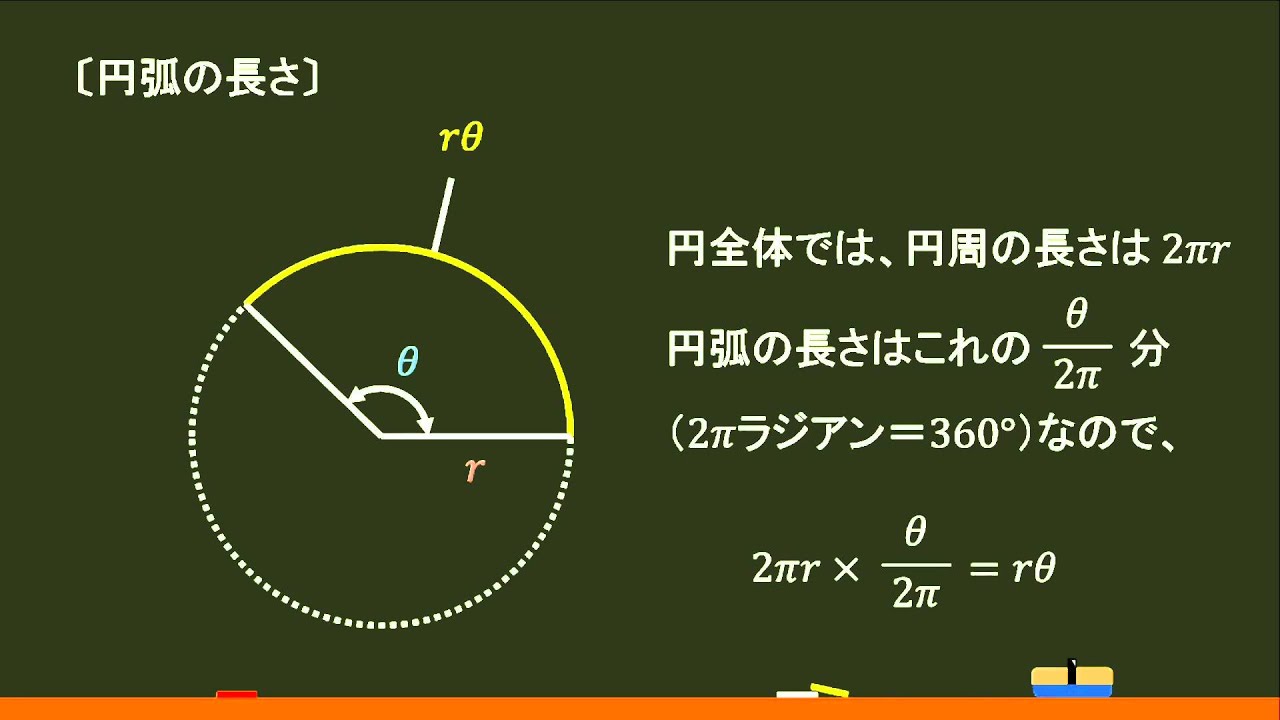
まずは、求めたい半径の大きさを ㎝とします。 すると、半径 ㎝で中心角1°の扇形の弧の長さは と表すことができます。 そして、弧の長さが ㎝になるはずだから という方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることが そんな公式はありません。 円の面積、円周の長さ、又は 扇型の中心の角度の どれか 1つが分かっていないと、 扇型の弧の長さから 半径を求めることは出来ませんし、 半径から 扇型の弧の長さを求めることも出来ません。扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 このページの続きでは、この 公式の導き方 と、 扇形の弧の長さを求める計算問題の解き方 を説明しています。 もくじ 扇形の弧の長さを求める公式 公式の導き方 扇形の弧の長さを求める計算問
扇形の面積・弧の長さの計算機です。 角度を入力 面積は 0 π です 弧の長さは 0 π です π=とした時 面積は 0 です 弧の長さは 0 です ※円周率πは無理数ですので数は参考値とされてください。 扇形の公式(計算式)扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。 ここで図形を 2πrっていうのは円周でしょ? 扇形の弧っていうのはその一部。 円周を360で割ると1°あたりの弧の長さになる。 例えば中心角が45°の扇形の弧の長さを求めるなら、それに45をかけてやればいい。 2πr÷360×中心角 というほうが考えやすいかも。
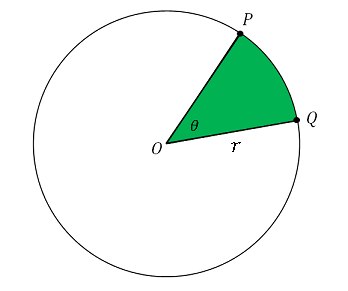
扇形の面積 = 弧の長さ × 半径 ÷ 2 なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。 では、どうしてこのようなことがいえるかを考えて見ましょう。 扇形の面積を求める公式は前に述べたとおり以下の公式です。 扇形の となります。もし 半径と弧の長さがわかっているのであれば 、その情報だけで 扇形の面積が出せる公式 です。便利なので覚えておくと楽な時があるかもですね。 兎にも角にもまずは弧の長さと面積を出せれば ok です。しっかり自分で追ってくださいね 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明 エンジニアの学習・コミュニティーサイト!




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち
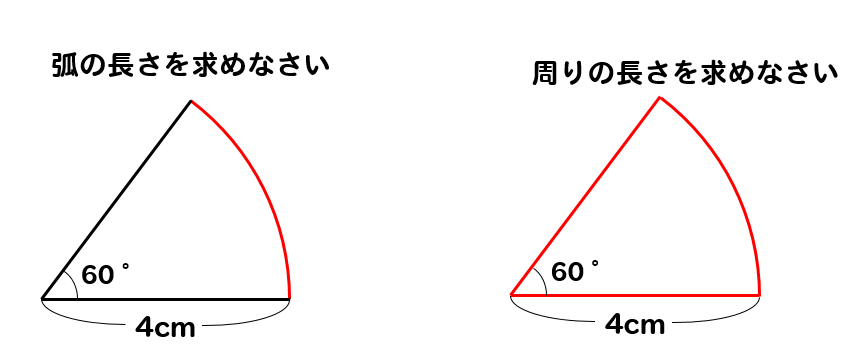



おうぎ形 注意 周りの長さを求める公式を解説 数スタ
なので、扇形の弧の長さは、 12 π × 1 360 = 4 π c m となります。 一般に、半径が r で中心角が α ∘ である扇形の弧の長さは、 2 π r × α 360 = π r α 180 となります。 弧度法の場合(つまり、中心角が θ ラジアンの場合)弧の長さは r θ となります。 弦の長さ 半径が 6 c m で、中心角が 1 ∘ である扇形の 弦の長さ を計算してみましょう。 弦は、二等辺三角形の底辺になります。 垂直二等分線 を扇形の弧の長さ L=rθ 扇形の面積 S=r^2θ/2=rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は?1分でわかる意味、公式、求め方、ラジアンとの関係 扇形の弧の長さと三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ
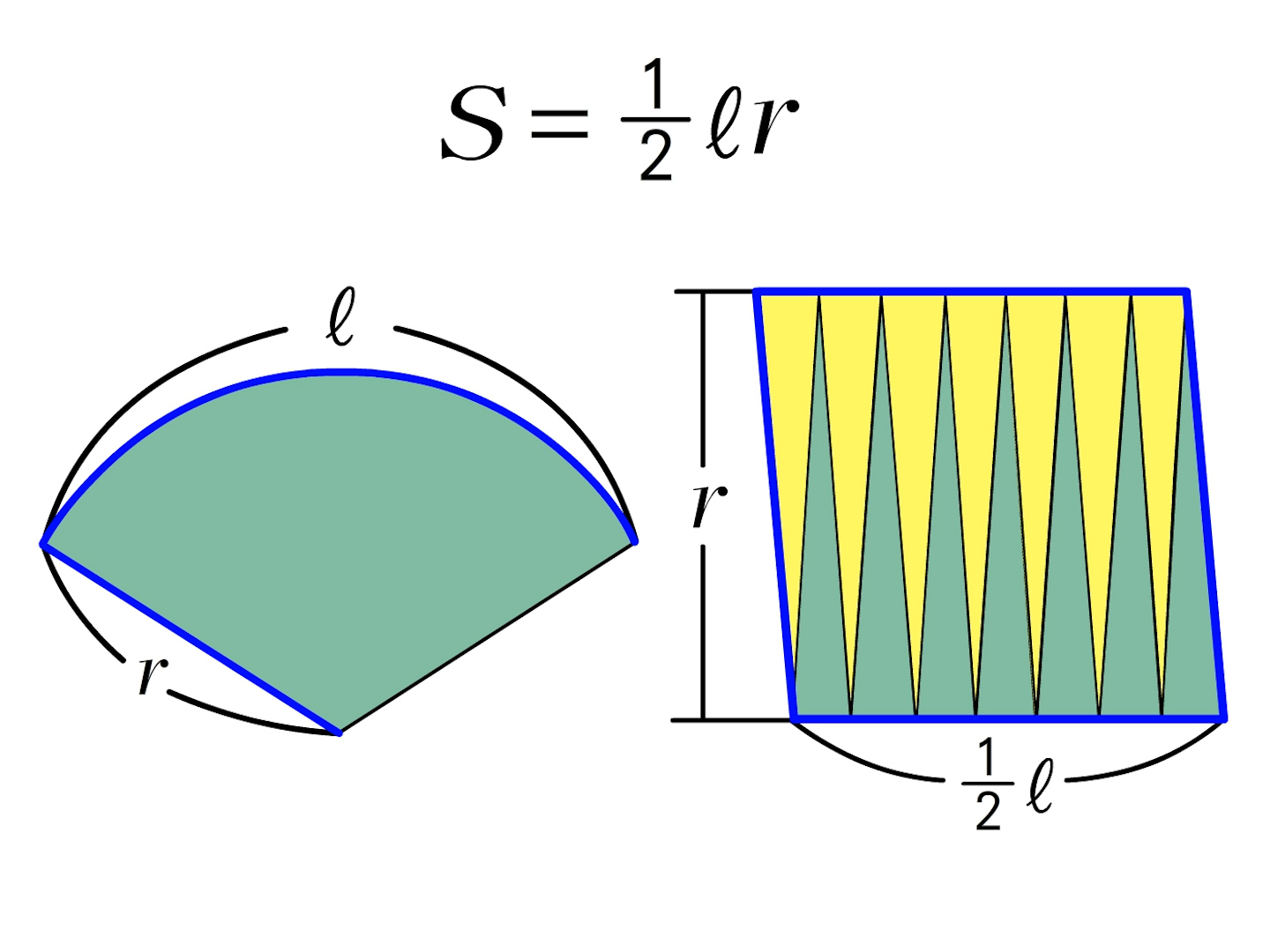
を考えていきたいと思います。 この公式のポイント ・ おうぎ形の面積は「1/2×弧の長さ×半径」 で求めることができます。 ・おうぎ形の半径をr、弧の長さをLとしたとき、面積Sは下の公式で書くことができます。 S = 1 2 l r ぴよ校長 おうぎ形は、半径 なので、 円周の長さ = 直径 × 円周率 となります。 おうぎ形の弧の長さ 円周の長さのうち 扇形は「円の 分の1」になっているかが重要です。 扇形の部分が円の「何分の1」なのかがわかれば簡単に解くことができます。 扇形の弧の長さの公式から方程式を立てます。 l=2πr× a 360 l = 2 π r × a 360 より、 2× π× 9× a 360=12π 2 × π × 9 × a 360 = 12 π a=240 a = 240 答えは 240° 問題4 半径 8cm 8 c m 、弧の長さ 6πcm 6 π c m の扇形の面積求めよ。 S=1 2lr=1 2 × 6π× 8=24π S = 1 2 l r = 1 2 × 6 π × 8 = 24 π 答えは 24πcm2 24 π c m 2 ちなみに円や扇形について、自由に印刷できる練習問題を



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋
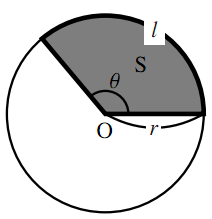



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
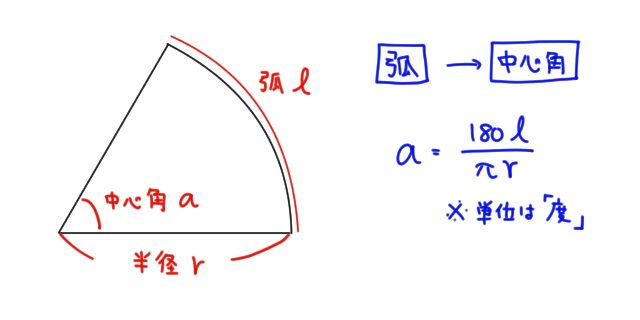
図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 面積 勉強法 家庭教師 平面上で円弧を睨む扇形の中心角を円弧の長さを使って定義しましたこのアイデアを全く同様に三次元に拡張したのが 立体角 です空間上半径 の球を考え球 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr になるってやつさ。 つまり、 扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができる んだ。 たとえば、 半径 4 cm、弧の長さが 6π cmの扇形があったとしよう。 この「扇形の中心角」を求めたいときは公式をつかえば一発。 3秒ぐらいで 弧度法 (radラジアン) 弧の長さで、角度を表す 円周と半径の割合は一定となる (円周を直径で割った時の値がπ) π = l 2 r l = 2 r π なので円周Lはπで表せる l = 2 r π 中心角Θの扇形の弧Lの長さもπで表せる




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋
こんにちは。今回は弧度法による扇形の弧の長さと面積について書いておきます。 扇形の公式はこう変わる 弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, なので、すこし見た目が変に思うかもしれませんが、 が答えとなります。 扇形の周の長さは、弧の長さを求めて半径を2つ分足すと完成。 中学生で を使った場合には、答えが式の形になります。 見た目が変になりますが、合っているので心配なく! ラジアンの求め方 弧度法 弧の長さは中心角に比例するのはイメージがつきます 円周は2πrなので 一周の中心角360°は2πradとなる とあります 1radを57,3として計算すれば360になるのはわかりますが、 360=2πradとなることがわかりません。
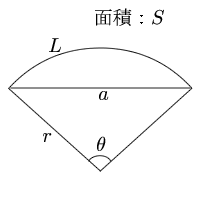



扇形 面積の計算 計算サイト




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
名前に「弧」とついているように,円の弧を使って定義します. 弧度法 半径1の扇形の弧の長さが θ であるとき,この扇形の中心角の大きさを θ rad と定める.ただし, rad は「ラジアン (radian)」と読む. 正確には,「円弧と半径が等しいときの中心角 扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめ 弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン
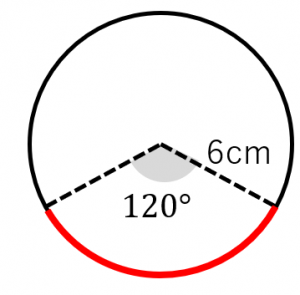



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師 面積 勉強法 家庭教師
円の直径と面積の公式では円周率を π とする 扇形の弧の長さと面積を出すためには、その前に円周と面積を必ず出さなければいけません。 そのため、小学校の算数のおさらいをしましょう。 円周や面積については、以下の公式によって計算しますしかし、実はこの問題をはるかに簡単に解くことのできる公式が存在します。 それは、扇形の面積をS、弧の長さをl、半径をrとおくと、 S=l×r÷2 (S=lr/2) これだけです。 上の問題で試してみると、 S=l×r÷2 =4π×5÷2 =10π 10πcm2 このように、全く同じ答えになることが分かります。 学校では教えてくれたりくれなかったりとまちまちなようですが、これを頭に入れておくと平面図形の問題だ長さ l d 直径から円周長 l d 円周長から直径 s d 面積から直径 長さ 円弧長 長さ h a θ s 底辺と高さ h θ b 高さ 長さ l θ h 底辺の長さ 長さ b a l 斜辺長 a θ l 斜辺長




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



おうぎ形まとめ 弧と面積の求め方 教遊者
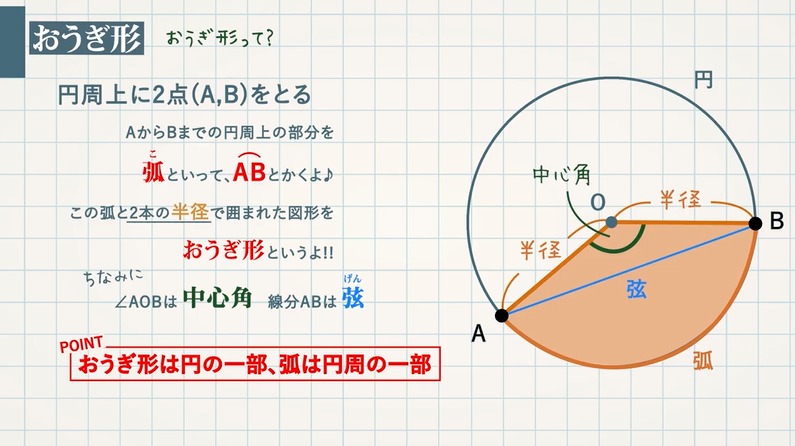
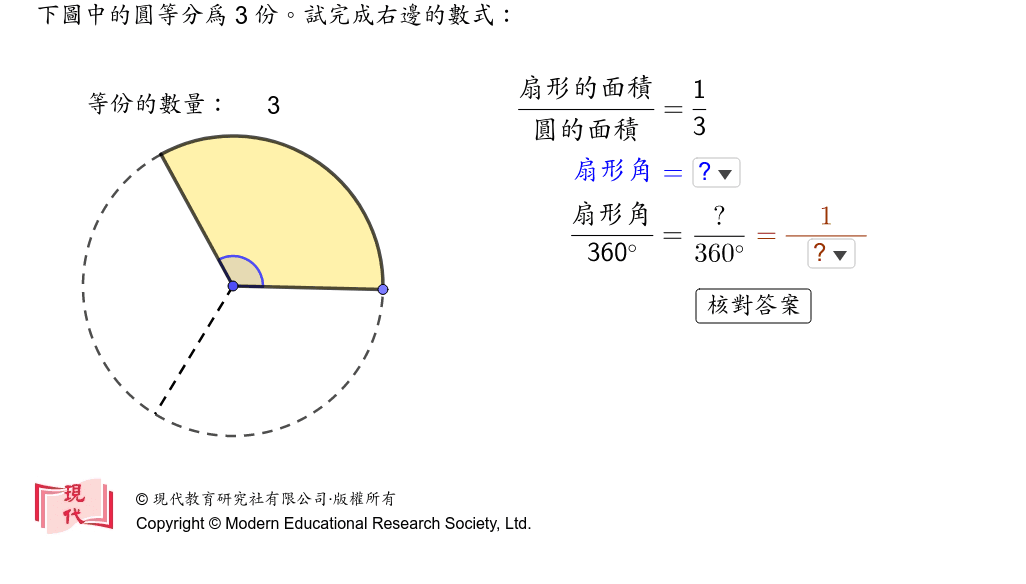
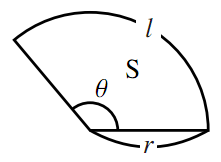
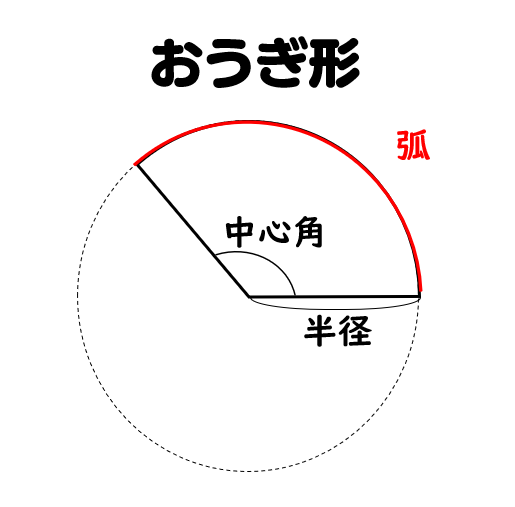
扇形の弧の長さ( l ength) 公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心角}}{360^\circ} $の割合をかけることで求められます。おうぎ形は弧と2つの半径に囲まれているので、弧の長さと半径×2が周りの長さになります。 弧の長さ:18×314× 150 360 150 360 =18×314× 5 12 5 12 =157×15=2355 ( cm c m) 半径×2:18 ( cm c m) 周りの長さ:=4155 ( cm c m) 問題3 半径6cmのおうぎ形の弧の長さが314cmだった。 この扇形の中心角の大きさを求めよ。 円周は12×314cm。 これに 中心角 360° 中 心 角 360 ° を ある扇形の半径は2cm、弧の長さは3cmです。この扇形の面積はいくらと計算できるでしょうか。 ・解答1 上のs=1/2lrの公式に当てはめていきます。 すると、 面積s=1/2 × 2 × 3 =3cm2と求められました。 まとめ s=1/2lrの公式の意味と計算方法




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル
扇形の半径を求めるときも、面積の公式または弧の長さの公式を利用します。 度数法の場合扇形の半径 角度が度数法で与えられた場合、扇形の半径は次のように求められます。 扇形の半径の求め方(度数法) 中心角 の扇形の半径 は、 面積 がわかっている場合 より 弧の長さ がわかっている場合 より 例題はここをクリック 弧度法の場合扇形の半径 角度が弧度法で与えられ扇形の面積が角度の大きさに比例することを利用して導いています。扇形の弧の長さlも、同様の関係を利用し l=rθ の式が誘導できます。よって、扇形の面積は下式で表すことも可能です。 s=r 2 θ/2=lr/2 扇形の弧の長さは、詳細は下記が参考になります。扇形の弧の長さと面積 半径 の円の円周上の,長さ の弧に対応する中心角を ラジアンとするとき, この ラジアンを単位とする角の大きさの表し方を 弧度法 というのであった. 以下では,角の大きさはすべて弧度法を用いて表す. 半径が の円において
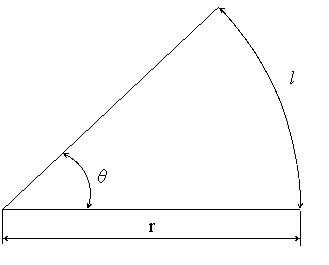



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
半径が 3 (cm)、中心角が 60° のおうぎ形の弧の長さを求めてください。 ただし円周率は 314とします。 おうぎ形の弧の長さを求める公式は おうぎ形の弧の長さ = 円周 中心角 × 中 心 角 360 ° なので、おうぎ形の弧の長さを L とすると L = 2 × 3 × 314 × 60



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典
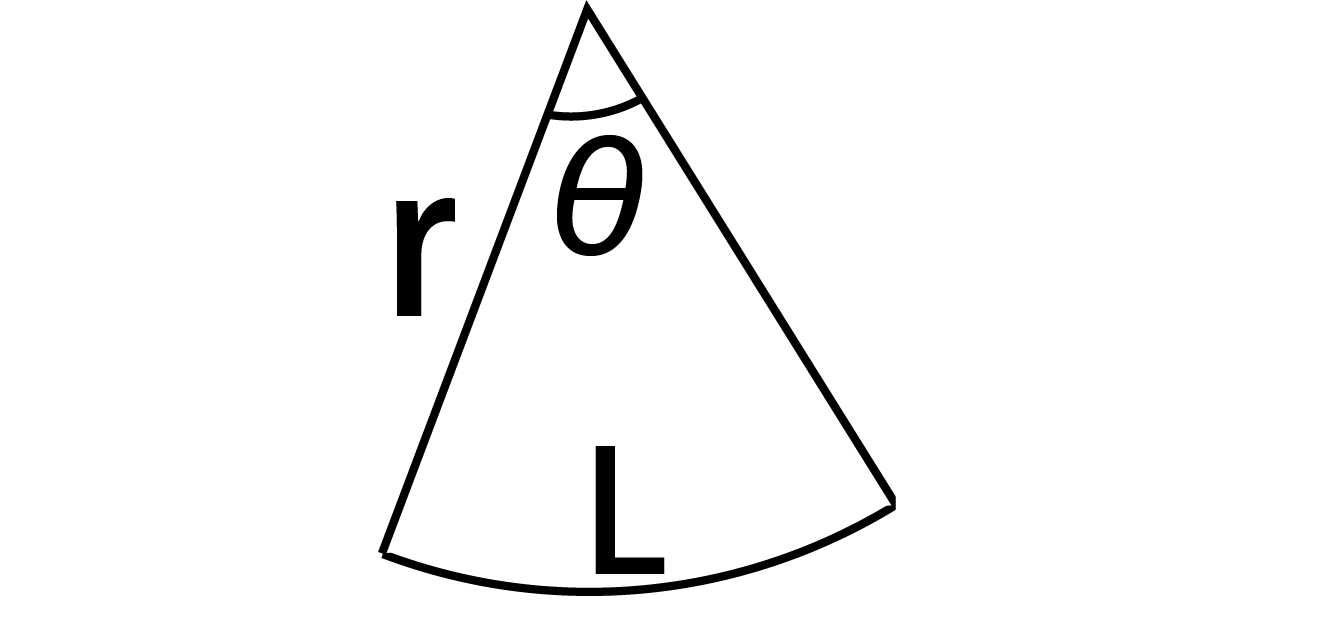



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
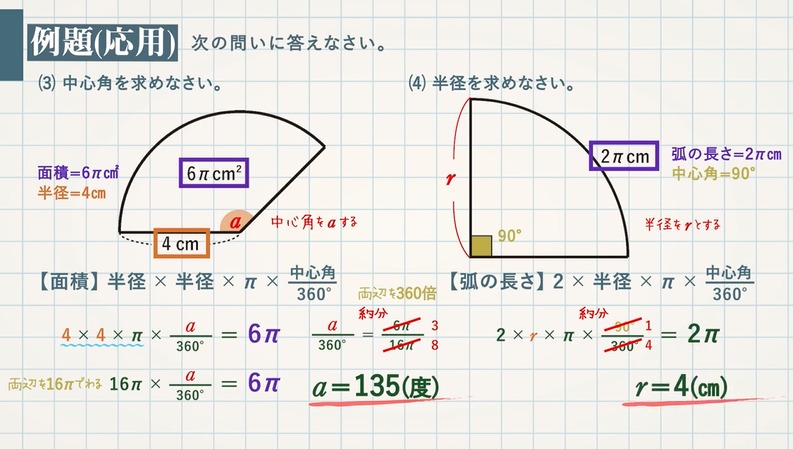



おうぎ形まとめ 弧と面積の求め方 教遊者




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく



扇形面積公式 Geogebra



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学



1年 おうぎ形の面積 数学イメージ動画集 大日本図書




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




充実 美徳 甘味 弦 と 弧 面積 克服する 部 悪意




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち



1



1




扇形の弧の長さの求め方 公式と計算例




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月



1
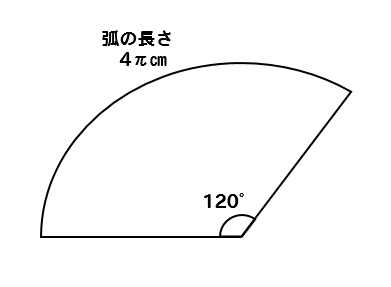



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
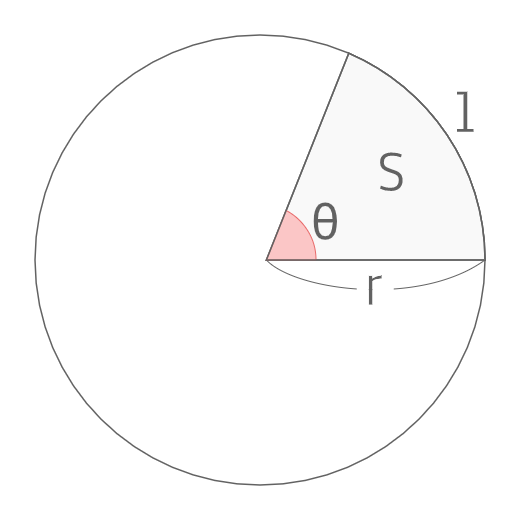



高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇形の弧の長さと面積 計算ドリル 問題集 数学fun




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




扇形の面積の求め方 公式と計算例




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形の面積 弧の長さ 計算機 かんたん計算機




扇形の弧の長さの求め方 公式と計算例
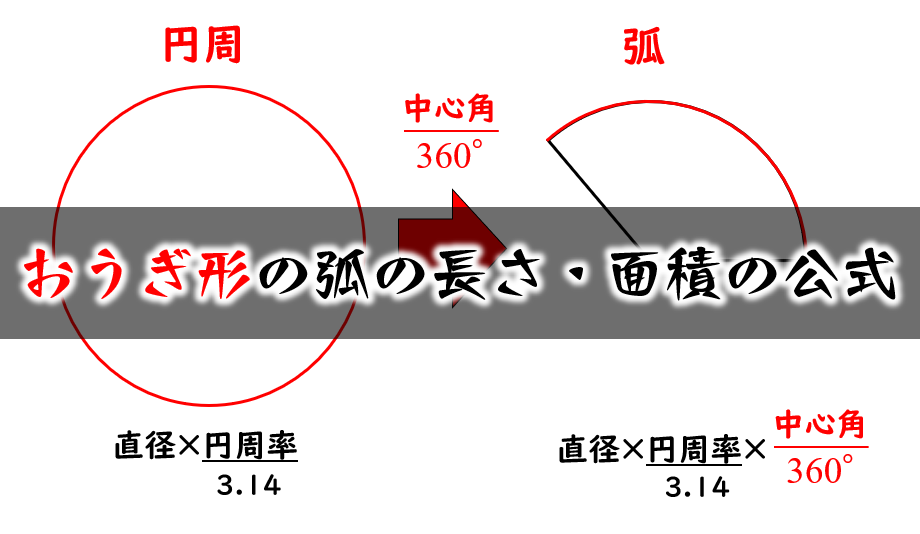



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
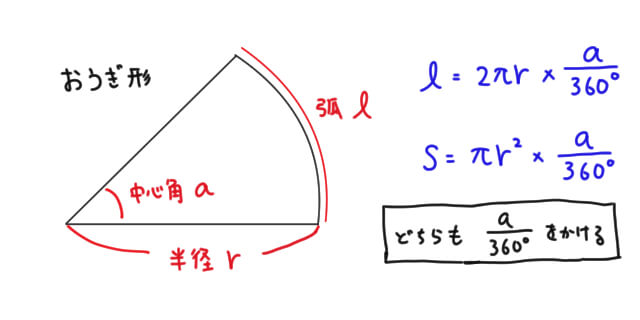



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




おうぎ形 注意 周りの長さを求める公式を解説 数スタ



半径4cm面積6pcm の扇形の中心角の求め方を教えてください Yahoo 知恵袋




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
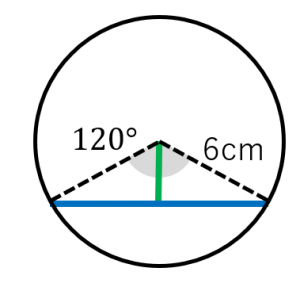



充実 美徳 甘味 弦 と 弧 面積 克服する 部 悪意




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




Download Qikeru Images For Free



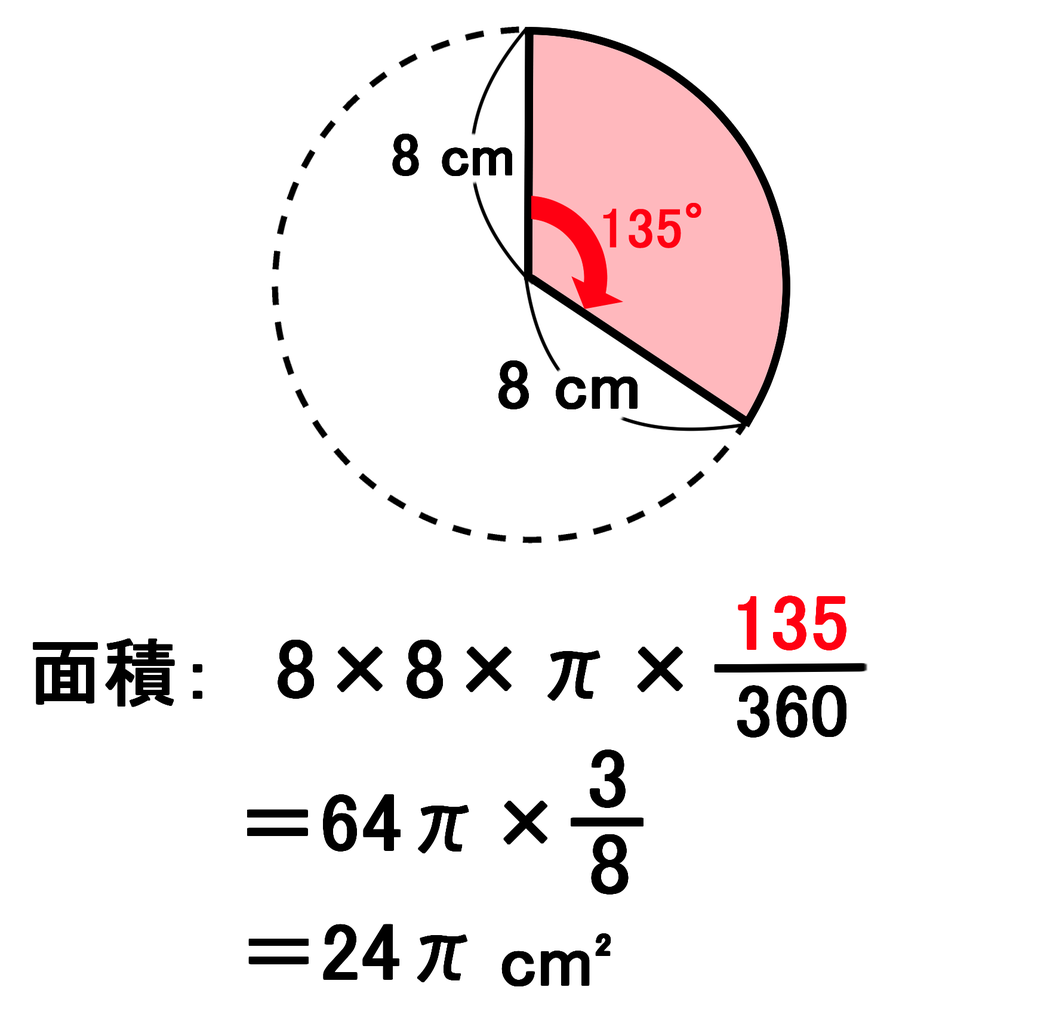
半径8cm 中心角135 のおうぎ形の弧の長さと面積を求めてくださ Yahoo 知恵袋




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張




公式が覚えられない を解消 円とおうぎ形の周りの長さ 面積の求め方 中学受験ナビ




円 扇形 の面積 周や弧の長さの公式 数学fun




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円 扇形 の面積 周や弧の長さの公式 数学fun




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



数 の三角関数の扇形の弧の長さと面積の公式の覚え方はあります Yahoo 知恵袋



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun



このサイト扇形の弧の長さの公式間違ってますよね 正しくは直径 円周率 Yahoo 知恵袋



1




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 数学 科学



扇形とは 面積 弧の長さ 中心角 半径の公式と求め方 受験辞典




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
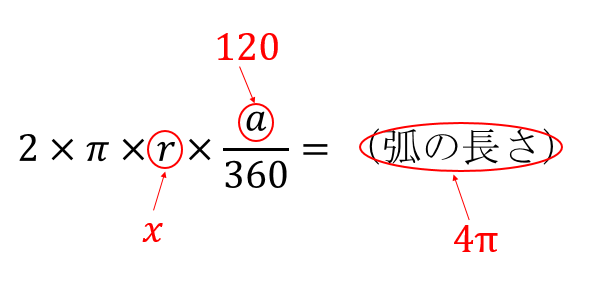



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形の弧の長さと面積 Excel Vba 数学教室




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube
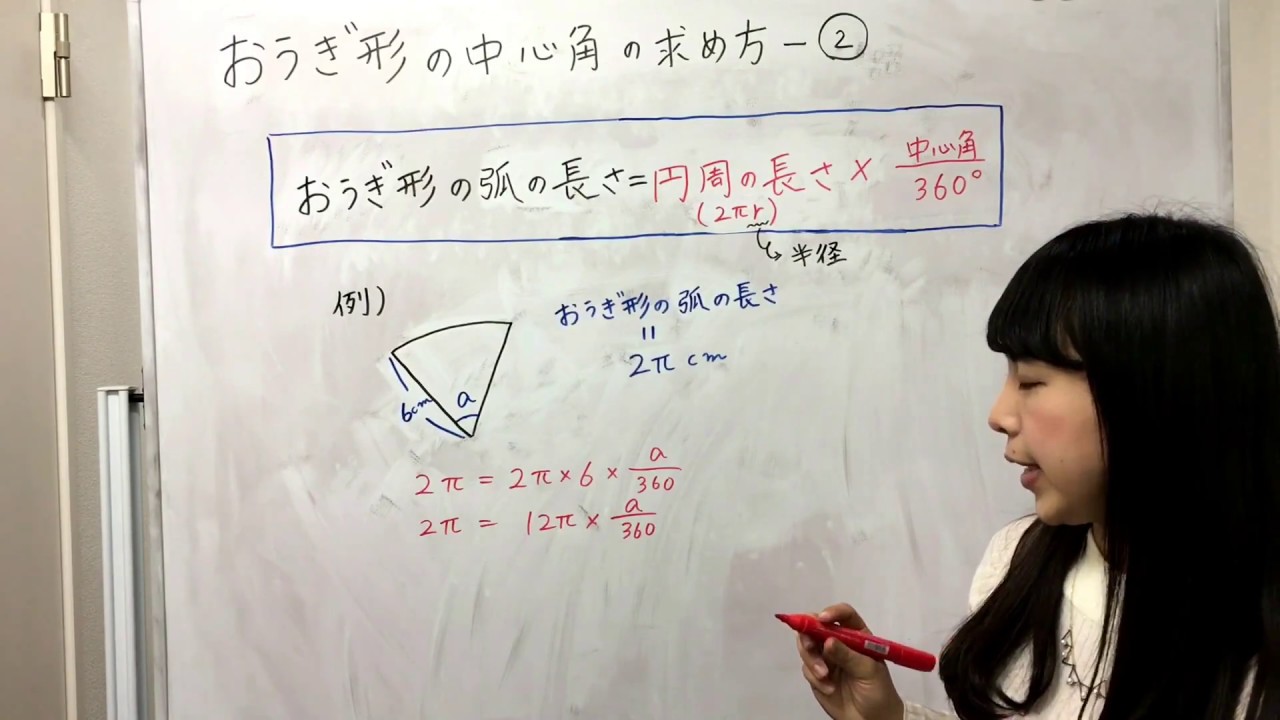



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube
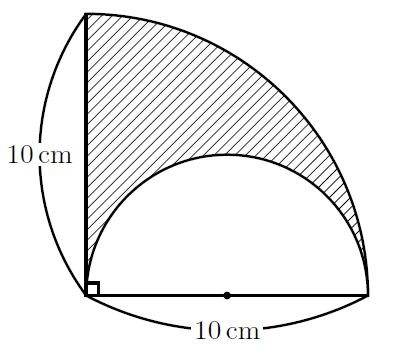



中学数学 扇形の面積 長さの瞬殺技 頻出図形 数樂管理人のブログ




円 扇形 の面積 周や弧の長さの公式 数学fun




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
コメント
コメントを投稿